Citat:
Milosh Milosavljevic1: Nedeljko, mislim da imas sitnu gresku u cetvrtom zadatku, ovaj integral je samo koren iz pi, a ne 2 korena iz pi. To si preneo i na deo pod b). Ja sam uspeo da uradim 4b) imitacijom dokaza Silvesterovog kriterijuma, okacicu moje resenje sutra, sad je isuvise mracno i mutna ispadne slika. Sto se tice petog, nismo ucili Zordanovu kanonsku formu, jel mozes da me uputis na neku literaturu?
Da, u pravu si za integral.
Žordanova kanonska forma treba da se uči iz linearne algebre. Ako polažeš analizu 2, to se valjda podrazumeva da je rađeno. Ako nije pogledaj
http://en.wikipedia.org/wiki/Jordan_normal_form
No, zadatak se može rešiti i bez toga. Neka je u preseku

-te vrste i
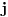
-te kolone broj
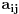
. Formiraj matricu B u kojoj je u preseku

-te vrste i
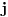
-te kolone broj
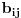
gde su
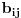
izabrani na sledeći način:
Za
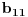
izaberi bilo koji transcedentan broj u

-okolini broja
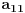
. To je moguće, jer je ta okolina neprebrojiva, a algebarskih brojeva ima prebrojivo mnogo.
Za
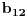
izaberi bilo koji broj koji je transcedentan nad poljem
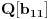
u

okolini broja
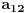
. To je moguće, jer algebarskih brojeva nad prebrojivim poljem ima prebrojivo mnogo, a ta okolina je neprebrojiva.
Nastavljajući postupak, dobijaš matricu B koja je u matričnoj normi bliska matrici A, a čije komponente ne zadovoljavaju nijedan algebarski zakon, tj. ne postoji nenula polinom sa
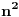
nepoznatih i racionalnim koeficijentima takav da kada se promenljive zamene komponentama matrice B vrednost polinoma bude 0, odnosno oni su algebarski neyavisni. Naime, indukcijom po k se dokazuje da su prvih k izabranih elemenata algebarski nezavisni.
Izabrani nenula polinom p sa racionalnim koeficijentima i k promenljivih predstavimo kao polinom po k-toj promenljivoj, čiji su koeficijenti polinomi po preostalim promenljivama. Jednostavno, za svako

grupišemo sve što ide uz
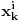
. Ako se dobije polinom koji uz
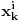
za

ima nule, tj. konstantan je u kao polinom po
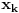
sa koeficijentima koji su polinomi po ostalim promenljivama, onda polinom p možemo zapisati tako da u njemu ne figuriše
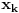
. U tom slučaju se tvrđenje svodi na induktivnu pretpostavku. U suprotnom, ako je p polinom po
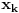
stepena bar 1, onda zamenimo u njemu sve promenljive osim
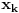
izabranim brojevima. Ako je uz
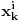
išao polinom sa racionalnim koeficijentima po ostalim promenljivama koji nije jednak nuli, onda na osnovu induktivne pretpostavke posle zamene ostalih promenljivih izabranim brojevima uz
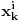
ide broj različit od nule koji pripada raširenju polja Q generisanom prethodno izabranim elementima. Dakle, pronašli smo polinom q stepena bar jedan, sa koeficijentima iz raširenja polja Q gnerisanim prethodno izabranim elementima, takav da je k-ti izabrani element koren tog polinoma, suprotno njegovom izboru.
Neka je

karakteristični polinom matrice B. Pretpostavimo da on ima bar jedan višestruki koren. U tom slučaju, polinomi

i
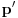
nisu uzajamno prosti, pa postoji njihov zajednički delilac

. Dakle,
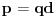
,
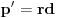
. Polinom

ima stepen ne veći od
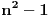
, a polinom

stepen ne veći od
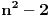
. Dakle, za neke brojeve
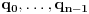
i
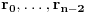
važi

,

.
No, svakako je
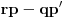
, što znači da su polinomi
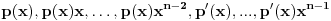
linearno zavisni. Ima ih
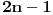
, a stepen im ne prelazi
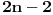
, pa se njihovi koeficijenti mogu smestiti u kvadratnu matricu reda
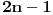
u kojoj se u preseku

-te vrste i
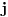
-te kolone nalazi koeficijent uz
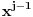
u

-tom polinomu iz niza. Obzirom da su vrste te kvadratne matrice linearno zavisne, ona će imati determinantu 0. Ovakva determinanta se zove rezolventa dva polinoma i ona je jednaka nuli akko polinomi imaju bar jedan zajednički koren.
Determinanta matrice je polinom po njenim komponentama, a komponente ove matrice su polinomi po komponentama matrice B. Zamislimo da smo na isti način formirali determinantu od kvadratne matrice C reda

, čije su komponente različite promenljive. Determinanta bi bila polinom po tim promenljivama sa racionalnim koeficijentima, ali ne nula polinom, jer za neki izbor promenljivih matrica nema višestrukih sopstvenih vrednosti. Stoga se determinanta dobijena od matrice B na isti način svodi na zamenu promenljivih u tom polinomu komponentama matrice B. Međutim, pošto se radi o nenula polinomu sa racionalnim koeficijentima, na osnovu izbora matrice B to ne može biti 0.
Dakle, matrica B ima samo jednostruke sopstvene vrednosti, pa je slična nekoj dijagonalnoj matrici D. No, u tom slučaju su matrice
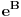
i
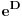
slične, pa imaju istu determinantu i isti trag. Ako se na dijagonali matrice

nalaze brojevi

, onda je
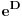
dijagonalna matrica sa brojevima

, pa je
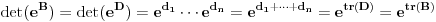
.
Obzirom da su determinanta i trag neprekidne funkcije,
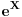
neprekidna matrična funkcija i matrica B bliska matrici A, onda je
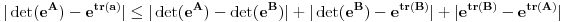
,
Drugi sabirak je 0, a prva dva se mogu izborom matrice B dovoljno bliske matrici A učiniti proizvoljno malim, pa jednakost važi u opštem slučaju.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
